 Eh beh, è il mio mestiere …
Eh beh, è il mio mestiere … 
In orbita circumlunare non avranno più i complicati problemi di protezione dalle radiazioni. Se le pigleranno tutte, e pace 
Ma stiamo parlando di consumo della ISS in LEO o di spostarla su Marte? È un casino leggere un topic quando si salta di palo in frasca ogni volta.
Ciao Cristiano, intanto scusa se non ho risposto prima come promesso, vengo subito al dunque e cerco di spiegare meglio cosa intendevo dire.
Tu sei partito da un dato ben preciso, ossia quell’accelerazione di 16,6 mm/s/giorno, e hai applicato la formula di Newton F=m*a per ricavarti la forza (in newton appunto) necessaria per produrre quella precisa accelerazione alla massa della stazione spaziale. Bene, come ti ho già detto questo tuo calcolo è stato effettuato correttamente, l’avevo ripetuto anche io, e produce appunto una forza di 0,0797 newton.
Chiaramente questo dato vale se quell’accelerazione è stata prodotta direttamente dall’applicazione di quella forza. Se ci sono altre componenti in gioco bisogna essere sicuri che non stiano interferendo con il fenomeno che vogliamo misurare.
E nel nostro caso c’è eccome una componente in gioco che sta interferendo, si tratta dell’energia orbitale specifica che è diminuita di una ben precisa entità, funzione della quota orbitale persa, della costante gravitazionale planetaria della Terra (G*massa Terra) e della massa della stazione spaziale ovviamente.
Siccome è difficile scrivere le formule in maniera chiara sul forum, almeno per me, ti invito a prenderle dalla rete direttamente.
Per concludere, è precisamente questa e null’altro l’energia che deve essere restituita alla stazione spaziale.
Un altro modo per arrivare ai valori corretti di propellenti necessari, potrebbe essere calcolare i due delta V per un trasferimento alla Hohmann che sollevi la quota orbitale della stazione di circa 300 metri, che mi pare sia la quota che la stazione perde ogni 10 giorni, e poi ovviamente moltiplicare tutto per 36,5 in modo da avere il valore annuale.
Ti va di provare questo calcolo?
Mi va sicuramente di provare, ma devo capire esattamente cosa calcolare e come calcolarlo.
Per la formula di cui parli, credo si possa prendere questa:
ma i calcoli come andrebbero fatti? Quali numeri devo usare per le tre variabili?
Ciao Aleph, abbozzo io una prima risposta…il discorso che fai è giusto ed è lo stesso che ho fatto anche io in un precedente post; andando nel merito ho effettuato il calcolo del deltaV considerando i valori ricavati dal grafico approssimati iniziali (per velocità e raggio orbitale) e finali (raggio orbitale) per una manovra alla Homann, ho diviso il risultato su un arco temporale di 21 giorni (dal grafico sembra questo l’intervallo temporale) e moltiplicato infine per i 365 giorni dell’anno. Il risultato come vedi dalla formula allegata è molto simile (10.4 m/s annui) siamo sugli stessi ordini di grandezza e la differenza ipotizzo sia sostanzialmente legata al modo visivo grossolano con cui ho estrapolato i dati dal grafico. A me la cosa sembrerebbe sensata in quanto il grafico in sé già porta in conto sia energia cinetica che potenziale gravitazionale (dal momento che riporta sia variazione di velocità che di raggio orbitale) e quindi sostanzialmente puoi “leggere” direttamente il deltaV dal grafico come ha fatto CristiaPi. Ovviamente non ho la certezza di aver fatto bene i conti né se siano corrette le conclusioni che ho riportato…
Non capisco la formula che hai usato, ma ho voluto provare a fare il tuo calcolo con le due formule riportate qui:
Dv1= 0,000141281 km/s
Dv2= 0,000141278 km/s
Dv1 + Dv2 = 0,000282559 km/s
circa la metà di quello che viene a te, per cui sarebbe ancora peggio, per il nostro discorso.
Ho semplicemente usato la conservazione dell’energia,la stessa formula che hai visto inizialmente su Wikipedia, allego formula per chiarezza
In effetti non avevo calcolato anche la ricircolarizzazione finale dell’orbita che comporta con i miei conti un 0.000136 km/s in più di deltaV e alla fine quindi circa 12.8 m/s annui totali…non so comunque dirti perrché i risultati sono diversi sinceramente non ho controllato i tuoi conti (e non ho la certezza di aver fatto bene i miei… XD)
Ok, mentre stavo scrivendo la risposta, ho appena letto la correzione; ho modificato la risposta. 
Ad ogni modo, sono comunque formule esatte solo per il caso ideale di orbite perfettamente circolari e prive d’interferenze. Sono ancora del parere che l’integrazione diretta dell’accelerazione rispetto al tempo sia la via più semplice e affidabile.
Aspetto comunque un eventuale chiarimento di Aleph su come usare il sistema da lui proposto. Quello che hai fatto tu è ciò che diceva Aleph?
Si è ciò che proponeva aleph.però ho continuato ad usare i dati che suggerisce il grafico (lui suggeriva di usare il dato di 300 m ogni 10 giorni) altrimenti perdiamo anche quel minimo di coerenza che ci resta…
Ok, perfetto. Di nuovo grazie a tutti per il concreto aiuto.
Cerca che ti ricerca, ho finalmente trovato alcune informazioni risolutive nel blog dell’ESA.
Qui http://blogs.esa.int/orion/2011/06/13/first-reboosts-complete/ si legge che il 12/6/2011 ci sono stati 2 mega-reboost; il deltaV totale è stato di 11 m/s con un guadagno di altitudine media pari a 19,3 km.
Graficando il semiasse maggiore medio e la velocità media ottenuti dai TLE, si vede chiaramente i vari reboost di quel periodo:
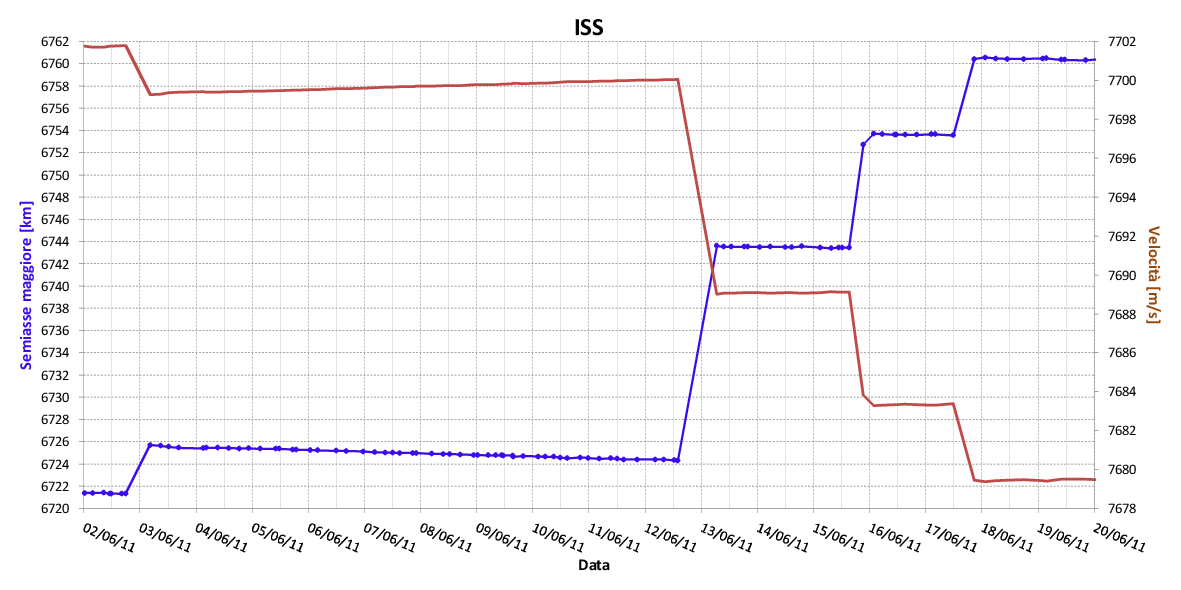
Invece di fare tanti calcoli, ho semplicemente provato a fare una sottrazione: velocità orbitale prima del reboost meno la velocità dopo del reboost: 7700,046 – 7689,065 = 10,981 m/s, incredibile!
Facendo una cosa simile per il semiasse maggiore: 6743,619 – 6724.342 = 19,277 km, ri-incredibile!
Calcoli confermati anche per il reboost successivo: http://blogs.esa.int/orion/2011/06/15/complete/, per il quale viene anche riportato il carburante consumato.
Direi che questo banale sistema è senz’altro validato e allora lo possiamo utilizzare anche per il grafico del post #35. Considerando sempre il primo segmento, la differenza di velocità dall’inizio della prima “rampa” alla fine della stessa è di 0,853 m/s, in buon accordo, quindi, con gli 0,8875 m/s risultanti da tutto il calcolo allucinante che m’ero messo in testa di fare.
Per dirla con un Grande, la soluzione deve essere più semplice possibile, purché non sia ancora più semplice. 
Automatizzando la procedura per i 7 reboost presenti nel grafico del post #35, ottengo 3,267 m/s.
Per il calcolo del consumo di carburante potrei usare la formula di Tsiolkovsky postata da lynott85 nel post #2 ottenendo 432 kg di carburante.
Volendo, invece, fare la proporzione con i dati del blog dell’ESA, potrei scrivere 796,2 / 5,75 * 3,267 = 452 kg; risultati abbastanza simili.
Be’, evidentemente per quest’anno si stanno dando al risparmio. 