Chiaro, ben leggibile, e spiegato BENE.
Grazie.
Ottimo articolo, come sempre.
La parte di geometria mi ha risvegliato un ricordo di qualche anno fa: nei dintorni di Amsterdam, sbagliai svincolo una decina di volte, a causa del gps che dava letteralmente i numeri, faceva avanti indietro di km e ogni tanto si spostava anche di lato 
Risolsi fermandomi e guardando la cara cartina, poi visto che cartina e cartelli non andavano proprio d’accordo (stanchezza, 15 ore di guida possono inficiare la capacità di leggere e scrivere), li abbiamo provati tutti fin che non ci siamo trovati al tanto sospirato capolinea della metro. Stessa trafila a Rotterdam e a random nelle campagne. ma ormai giravamo a naso, il gps era acceso per compagnia/goliardia. In pratica lo abbiamo eletto a scemo del villaggio, da prendere per il beep perchè non sa dov’è. 
Usavamo Sygic (Offline, PAGATO e aggiornato) su un Iphone, ma anche google maps non era da meno in quanto a svarionamenti.
Da allora ho il dubbio/certezza che il GPS non vada d’accordo con i punti al di sotto del livello del mare: bisogna armarsi di pazienza, cartina, bussola e chiedometro.
Edit: con GPS in difficoltà, intendo l’architettura software dei ricevitori, per il quale (imho) ci si può trovare solo sulla superficie di una sfera o su un punto sopra di essa, non sotto.
Penso che dal lato dei satelliti GPS non ci sia nessun miglioramento da fare un questo senso, ma solo migliorare i ricevitori.
In realtà i punti di intersezione sono più frequentemente ad alta quota che non sottoterra, e separati di molti km, per cui il ricevitore non dovrebbe avere problemi. Magari era disturbato da qualcosa. Con quelli moderni che includono il Glonass è ben più difficile, le frequenze sono diverse, e le soluzioni “strane” vengono scartate. E se volete una conferenza colta su GDOP, PDOP, sferoidi e WGS84 abbiamo anche quelli… l’ho appena sfiorata, ma la matematica del GPS è piuttosto tosta.
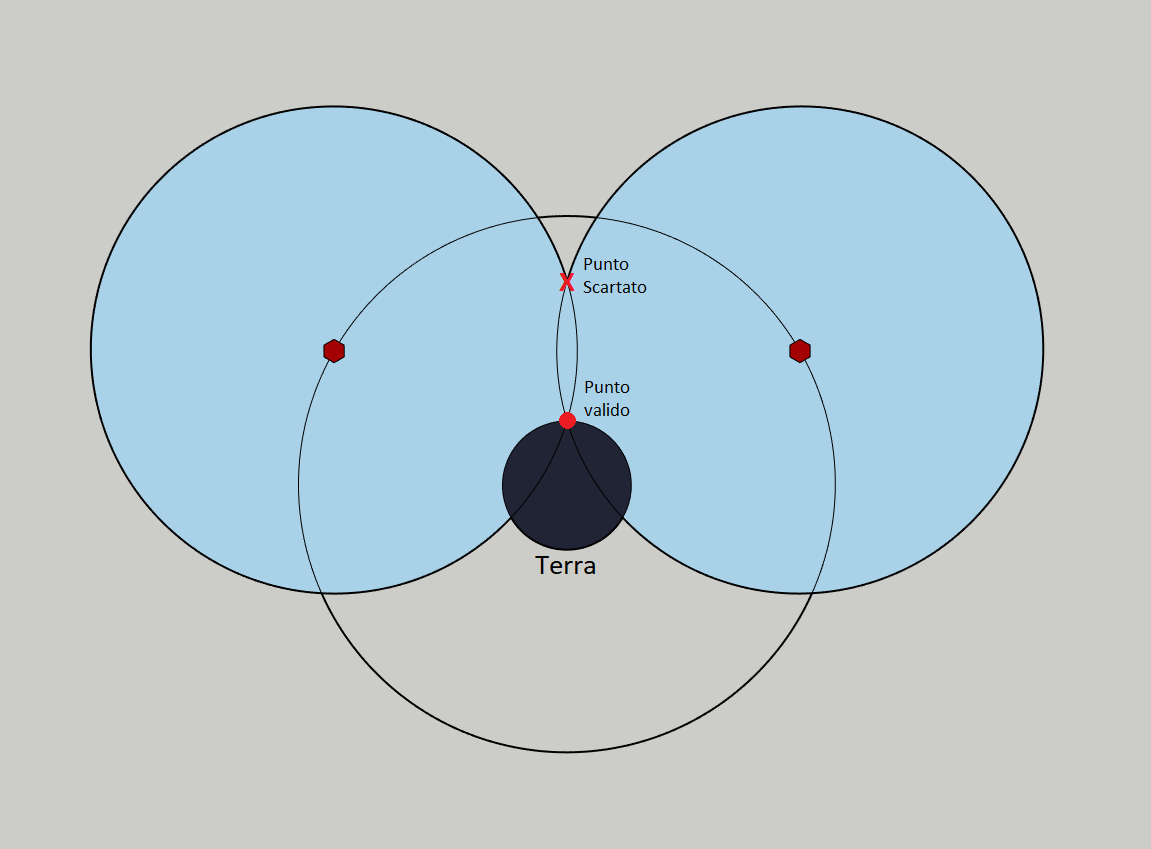
Il mio amico continua fare fatica a immaginare come il secondo punto di intersezione (quello da rigettare) possa trovarsi sotto la superficie terrestre… 
Anche supponendo i satelliti molto più distanti e molto bassi all’orizzonte, gli pare sempre che debba trovarsi sopra. Come andrebbe modificata questa figura per ottenere un tale risultato?
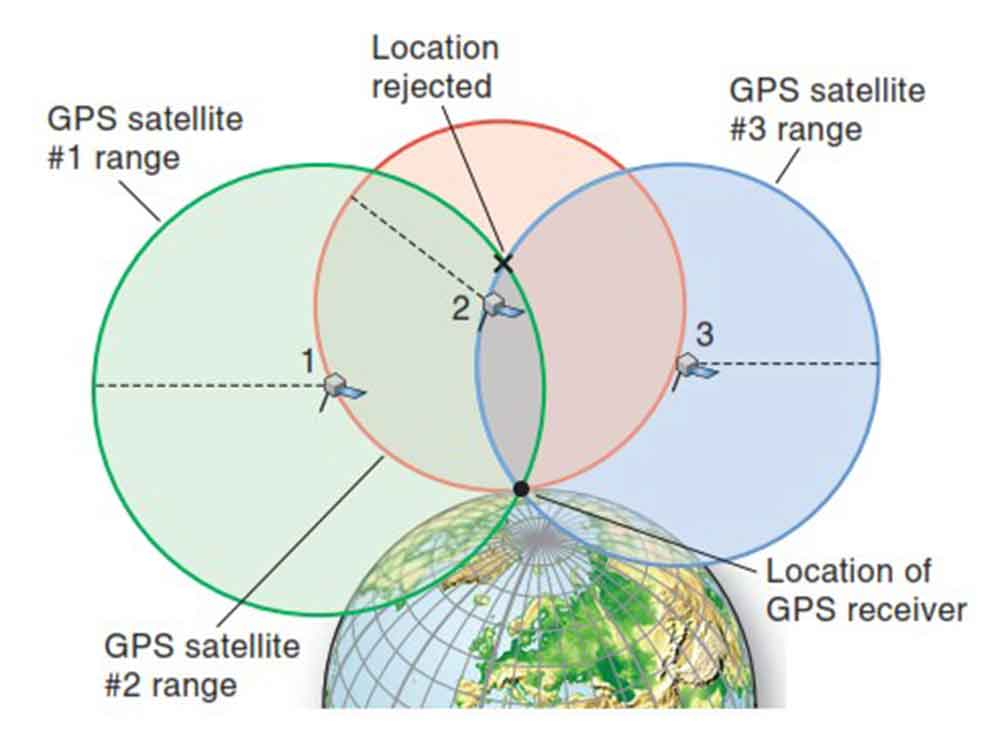
Per facilitargli il ragionamento, è corretto pensare solo a due sfere e al cerchio determinato dalla loro intersezione? La terza sfera non fa che identificare due punti su tale cerchio, no?
Sì, Roberto, hai ragione. Il punto inferiore potrebbe essere sotto la superfice solo se i satelliti fossero sotto l’orizzonte (ma allora ovviamente non li riceveresti). Mi sa che ho preso una papera 
Per quanto riguarda il disegno e i punti di intersezione, il disegno è un po fuorviante perché i satelliti GPS stanno in orbita MEO quindi almeno tre volte il diametro della terra…se riesco in giornata faccio un disegno…
Anche io, che pensavo di aver capito, ho dei dubbi.
In maniera molto grezza e per quel poco che mi ricordo di trigonometria e onde radio io la interpreto così.
Le tre ipotetiche sfere, associate ai satelliti, intersecano un punto sulla superficie terrestre.
Conoscendo la distanza dal satellite in orbita, calcolo il tempo che ogni segnale impiega a raggiungere il mio ricevitore e riesco a “triangolare” la posizione del punto dove mi trovo.
Spero sia più o meno così altrimenti mi tocca rispolverare i libri di geometria e di trasmissioni dei segnali radio.
Beh un po’ meno. I satelliti orbitano a 20.180 Km e il diametro della Terra è di 12.742. Quindi orbitano ad una altezza che è meno del doppio del diametro del pianeta.
Salvo, è così. Due sfere si intersecano in in cerchio, che definisce un piano. Tre sfere si intersecano in due punti, e uno dei due è quello buono. Che poi il disegno non sia in scala, è ovvio.
Ecco qui ho fatto un disegno con le proporzioni giuste.
Il disegno è più chiaro in 2D, poi completarlo col pensiero è facile, seguitemi:
Due superfici sferiche si intersecano in una circonferenza. Una circonferenza interseca una terza superficie sferica (diversa dalle prime due) in due punti.
Facile, no?
Edit: ho visto ora la risposta di Marco, quindi riconfermo!
La cosa interessante è che se volete l’accuratezza di posizionamento a 3 metri dovete misurare l’orologio di bordo, il tempo di arrivo del segnale, la posizione del satellite, e le correzioni relativistiche, con incertezza totale delle misure di tre metri: 10 miliardesimi di secondo, 10 ns, che è il tempo che l’onda elettromagnetica ci mette a fare 3 m. E’ questa incredibile precisione che rende quasi magici i sistemi di posizionamento satellitare.
Grazie. Molto chiaro, mi rendo conto che un ripasso di geometria non farebbe male.
@Sinuceup, praticamente
